Head First Statistics

Frequency Density

= Frequency / Group width

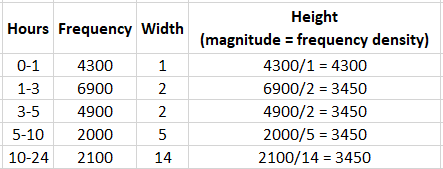
Cumulative Frequency

Mean

$$ \mu = \frac{\sum_{i=1} x_i }{ n } $$

$$ \mu = \frac{\sum_{i=1} f_i, x_i }{ \sum_{i=1} f_i } $$

where $f_i$ denotes frequency of $x_i$ (e.g. $x_i$ can denote a certain age, and $f_i$ is #people belonging to that age).

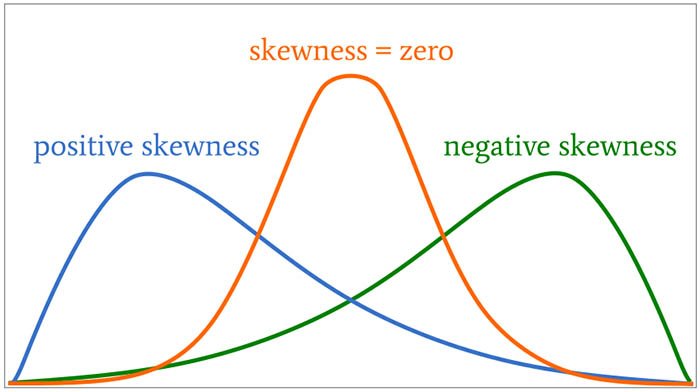
Skewed Data

When outliers pull the mean of the data to the left or right:

Average

There are several kinds of average: 1) mean, 2) median, 3) mode.

Mode

The mode refers to the most frequent value. If there are two modes, the data is called bimodal. It even works with categorical data, a class with the highest frequency is called modal class.

Quartiles

It is used to deal with outliers which mess with lower and upper bounds. The values that split data into quarters (4 chunks) are known as quartiles. Finding quartiles is a bit like finding the median. Instead of finding the value that splits data in half, we are finding values that split data into quarters.

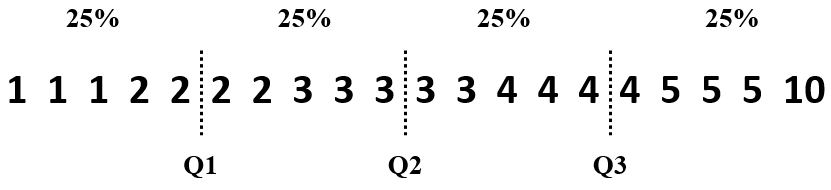
Example to further explain the quartiles

where Q1, Q2, and Q3 stand for first, second, and third quartiles, where Q2 is the same as the median, and Q1 and Q3 are also called lower and upper quartiles.

Interquartile Range (IQR) = Q3 - Q1. The IQR gives us a standard, repeatable way of measuring how values are dispersed. This range contains 50% of data dispersed from the middle point.

The upper and lower quartiles are positioned so that the lower quartile has 25% of data below it, and the upper quartile has 25% of data above it. This means that the interquartile range (IQR) only uses the central 50% of data, so outliers are disregarded. By only considering values around the center of data, we automatically exclude any outliers.

Percentiles

If you break up a set of data into percentages, the values that split the data are called percentiles.

 

Quartiles are actually a type of percentile. The lower quartile is $P_{25}$, and the upper quartile is $P_{75}$. The median is $P_{50}$.

Variance

We want to calculate average distance of data from the mean to measure variability. The equation for the variance is:

$$ \sigma^2 = \frac{ \sum_{i}^n (x_i - \bar{x})^2 }{ n } $$

Alternative to the above equation is:

$$ \sigma^2 = \frac{ \sum_{i}^n x_i^2 }{n} - \bar{x}^2 $$

Standard Deviation

What we really want is a number that gives the spread in terms of the istane from the mean, not distance squared. Then, standard deviation $\sigma$ = $\sqrt{varaince}$.

Standard Score (z-score)

The standard score gives you a way of comparing values across different sets of data where mean and standard deviation differ. The standard score is calculated as:

$$ z_i = \frac{x_i = \mu}{\sigma} $$

A standard score transforms each set of data into a more generic distribution where $\mu=0, \sigma=1$.

A statistician may say that a particular value is within one standard deviation of the mean, which refers to a range from $\mu - \sigma$ to $\mu + \sigma$ takes 64% of the distribution.

We have seen that using z-scores transforms your dataset into a generic distribution with a mean of 0 and a standard deviation of 1. If a value is within 1 standard deviation of the mean, this tells us that the standard score of the value is between -1 and 1.

Probability

Probability of winning for a roulette?

$$ Pr = \frac{#ways \: of \: winning }{ #possible \: outcomes } $$

In general, $Pr(A) = \frac{ n(A) }{ n(S) }$ where $n(A)$ and $n(S)$ refer to a number of ways of getting an event A and a number of possible outcomes. $S$ is known as the probability space or sample space. The possible events are all subsets of $S$.

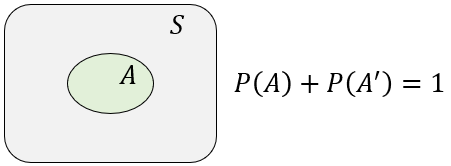
An important thing to remember is that a probability indicates a long-term trend only.

Some Notations

Intersection: $\cap$

Union: $\cup$

Note that $P(A \cup B) = P(A) + P(B) - P(A \cap B)$.

If $A$ and $B$ are mutually exclusive : $P(A \cap B) = 0$. If $A$ and $B$ are exhaustive, then $P(A \cup B) = 1$.

Conditional Probability

Probability of event A occurring given event B: $P(A | B)$.

$$ P(A|B) = \frac{ P(A \cap B) }{ P(B) } $$

We can modify the above equation by using $P(A \cap B) = P(A | B) P(B) $ and $P(B \cap A) = P(B | A) P(A)$.

$$ P(A | B) = \frac{ P(B|A) P(A) }{P(B)} $$

Visualize Conditional Probabilities with a Probability Tree

For instance, a probability three of a Roulette Game is:

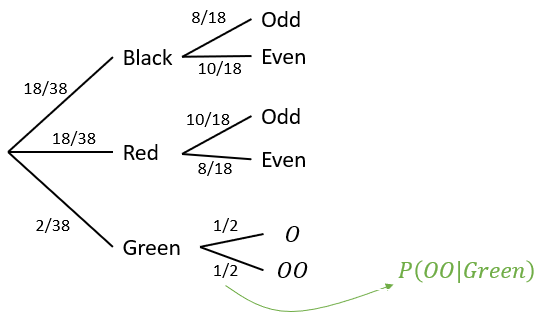
Probability Tree. Note that the probability for each set of branches must add up to 1.

The first set of branches shows the probability of each outcome. The second set of branches shows the probability f outcomes given the outcomes of the branch it is liked to. Each set of branches must add up to1.

Probability Tree Helps You Calculate Conditional Probabilities

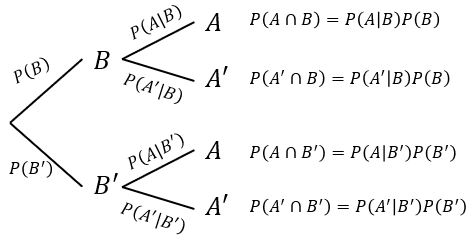
A general form of the probability tree

Example of the probability tree

Law of the Total Probability

Let the probability tree be

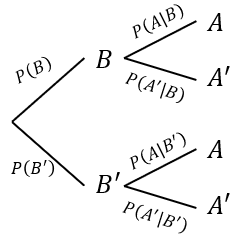
And we want to calculate $P(B|A)$:

$$ P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{ P(A|B)P(B) }{ P(A) }  \tag{1} $$

where the numerator can easily be calculated, but how do we calculate the denominator? To find $P(A)$, we need to add up the probabilities of all the different ways in which the event we want can possibly happen. There are two ways in which event $A$ can occur: Either with event $B$ or without it. Then,

$$ P(A) = P(A \cap B) + P(A \cap B^{\prime}) $$

$$ = P(A|B)P(B) + P(A|B^{\prime})P(B^{\prime})  \tag{2}$$

The above equation is termed the law of the total probability.

Introduction to Bayes' Theorem

We already know $P(B), P(A|B)$, and$P(A|B^{\prime})$. We want to compute the reverse of what we already knew: $P(B | A)$.

If we substitute $Eq.(2)$ into $Eq.(1)$, we obtain:

$$ P(B|A) = \frac{ P(A|B) P(B) }{ P(A|B)P(B) + P(A|B^{\prime})P(B^{\prime}) } $$

The above equation represents the Bayes' theorem. The Bayes' theorem gives you a means of finding reverse conditional probabilities.

Dependency & Independency

Example #1

Let's think about the roulette game.

$$P(Even | Black) = 10/18 = 0.556  \tag{3} $$

$$ P(Even) = 18/38 = 0.474  \tag{4} $$

$Eq.(3)$ and $Eq.(4)$ are different, and it shows that event $Even$ is affected by event $Black$. In general terms, events $A$ and $B$ are said to be dependent if $P(A|B)$ is different from $P(A)$.

Example #2

Let's think about rolling a =fair dice. What is the probability of getting $2$ after $1$? Namely, $P(2 | 1)$. 

Since getting $1$ and $2$ are independent, $P(2 | 1)$ can be reduced to $P(2)$. In general terms, if events $A$ and $B$ are independent, then the probability of $A$ is unaffected by event $B$. In other words,

$$ P(A | B) = P(A) $$

 

We know that $P(A \cap B) = P(A|B) P(B)$ or $P(B|A) P(A)$. But if events A and B are independent, $P(A|B) = P(A)$ and $P(B|A)=P(B)$. Therefore, 

$$ P(A \cap B) = P(A|B)P(B) = P(A)P(B) $$

Example #3

Are the yoga and swimming classes dependent or independent?

$$P(Yoga)=1/3, \: P(Swimming)=3/4, \: P(Yoga \cap Swimming)=1/4$$

If they are independent, $P(Yoga \cap Swimming) = P(Yoga) P(Swimming)$ must be satisfied. Since they are satisfied, $Yoga$ and $Swimming$ are independent.

Expectation

Example #1

Compute long-term earnings from a slot machine. The winning and probabilities for each item are as follows:

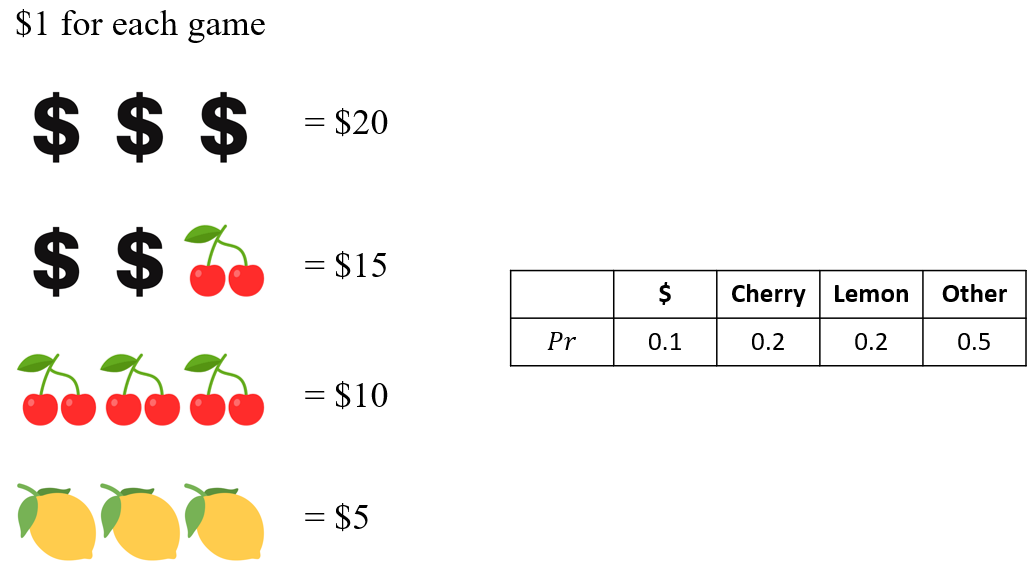
Then, probability of winning is as follows:

Then, the chance of winning anything is: 0.001 + 0006 + 0.008 + 0.008 = 0.023. Then, the change of losing is: 1 - 0.023 = 0.977. Now the probability distribution of earning is as follows:

Expectation $E(X) = \sum_i^n x_i P(x_i) = (-1 \times 0.977) + \cdots + (20 \times 0.001) = -0.77$. This is the expected earning from the 1 dollar bet.

Variance of Expectation

Expectation gives the typical or average value of a variable but id eos not tell you anything about how the values are spread. We can use the variance formula for this too,

• The original variance formula: $ \frac{ \sum_i^n (x_i - \bar{\mu})^2 }{ n } $. 
• The variance of the expectation: $ \sum_i^n P(x_i) (x_i - \mu)^2 $, where $\mu$ is $E(X)$. Again, it can reduced to $E(X - \mu)^2$.

The variance of expectation of the slot machine is: 

$$ 0.977(-1 - (-0.77)) + 0.008( 5 - (-0.77)) + \cdots + 0.001(20 - (-0.77)) = 2.6971  $$

Then, its standard deviation is: $\sqrt{2.6971} = 1.642$. This means that our winnings per game will be 1.642 away from the expectation of -0.77.

Linear Transformation of Expectation and Variance

Let's say the cost of each game has gone up to $2, and the prize are now five times higher than before.

The original gain $X$ and the new gain $Y$ can be represented as:

$$X = (original \: win) - (original \: cost)  \tag{5}$$

$$Y = 5(original \: win) - 2(original \: cost)  \tag{6}$$

If we substitute $(original \: win) = X + (original \: cost)$ from $Eq.(5)$ into $Eq.(6)$, we obtain:

$$ Y = 5X + 3(original \: cost) $$

Since the original cost is $1, the above equation can be reduced to:

$$ Y = 5X + 3 $$

In general terms,

$$ E(Y) = E(aX + b) = aE(X) + b $$

$$ Var(Y) = Var(aX + b) = a^2 Var(X) $$

Therefore, $E(Y) = 5 E(X) + 3$ and $Var(Y) = Var(aX + b) = a^2 Var(X)$. The linear transformation of $E(X)$ and $Var(X)$ is possible when underlying probabilities are the same, but only the values are different.

Independent Multiple Obsrevations

What if you were going to play two slot machines at the same time? Let's say the one slot machine's probability distribution is as follows:

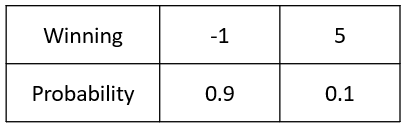
Table 1

Then the probability distribution of the two slot machines is:

Table 2

So, how do we find $Table1$'s expectation and variance based on $Table2$? Playing two slot machines is like having two observations at the same time: $X_1$ and $X_2$ from $X$, where $X_1$ and $X_2$ refer to random variables for first and second observations. Then, what we want to calculate is $E(X_1 + X_2)$ and $Var(X_1 + X_2)$:

$$ E(X_1 + X_2) = E(X_1) + E(X_2) = E(X) + E(X) = 2E(X) $$

$$ Var(X_1 + X_2) = \cdots = 2Var(X) $$

What about $E(X + Y)$ and $Var(X+Y)$?

What happens if we play two different machines with two different probability distributions at once? 

Let random variables to represent the machine#1 and the machine#2 be $X$ and $Y$. 

There are two possible solutions:

1) Calculate the probability distribution with every possible combination of $X$ and $Y$ and compute $E(X)$ and $Var(X+Y)$. While this is possible, but too much burden.

2) We can use the following formula (this is possible only if $X$ and $Y$ are independent):

$$E(X+Y) = E(X) + E(Y)$$

$$ Var(X + Y) = Var(X) + Var(Y) $$

 

$E(X-Y)$ is also possible:

$$ E(X-Y) = E(X) - E(Y) $$

$$ Var(X-Y) = Var(X) + Var(Y) $$

Note that the variability always increases if we compute combinations of two random variables.

 

You can also add and subtract linear transformation:

$$ E(aX + bY) = aE(X) + bE(Y) $$

$$ Var(aX + bY) = a^2 Var(X) + b^2 Var(Y) $$

$$ E(aX - bY) = aE(X) - bE(Y) $$

$$ Var(aX - bY) = a^2 Var(X) + b^2 Var(Y) $$

Factorial

• Counting every possible arrangement in line: $n!$
• Counting every possible arrangement in circle: $(n-1)!$ since we fix one as a starting point

Arranging Duplicates

Imagine you need to count a number of ways in which $n$ objects can be arranged, where $k$ objects are alike. The number of arrangements is 

$$ \frac{n!}{k!} $$

What if there are $k$ of one type are alike and $j$ of another type are alike:

$$ \frac{n!}{k! j!} $$

In general, when calculating arrangements that include duplicate objects, divide the total number of arrangements $n!$ by the number of arrangements of each set of alike objects $j!, \: k!, \: and \: so \: on$.

Example

There are 3 horses, 2 zebras, and 5 camels. What is the probability that all 5 camels finish the race consecutively if each animal has an equal chance of winning?

Solution: 

$$ \frac{ \# arrangements \: in \: which \: all \: the \: camels \: are \: together }{ \# arrangements \: of \: all \: the \: species } $$

The numerator can be calculated by $\frac{10!}{3!2!5!}$.

The denominator can be calculated by $\frac{6!}{3!2!}$ as we consider 5 camels as one object, then we have 3 horses, 2 zebras, 1 group of 5 camels. 

Permutation

Example

There are 20 horses. How many ways can we fill the top three hoses?: $20 \times 19 \times 18 = 6840$. The solution can be generalized as:

$$ 20 \times 19 \times 18 = \frac{20 \times 19 \times 18 \times (17 \times 16 \cdots 1)}{(17 \times 16 \cdots 1)} = \frac{20!}{17!} $$

The numbre of arrangmeents of 3 objects taken from 20 is called the number of permutations.

In general, the number of permutations of $r$ objects taken from $n$ is written as:

$$ ^{n}P_{r} = \frac{n!}{ (n-r)! } $$

Combination

This time, we want to know a number of combinations of the top three horses. As for the combinations, an exact arrangement does not matter. The number of permutations includes the number of ways of arranging the three horses that are in the top three. There are 3! ways of arranging each set of 3 horses, so let's divide the number of premutation by 3! This will give you the number of ways in which the top three positions can be filled bu without the exact order mattering. The result is:

$$ \frac{20!}{3! 17!} $$ 

In general, the number of combinations is the number of ways of choosing $r$ objects from $n$ without needing to know the exact order of objects:

$^{n}C_{r} = \frac{n!}{r! (n-r)!}$

Geometric Distribution

Example

You are playing a game. The probabilities of success and failure are 0.2 and 0.8, respectively. What is the probability of winning within two trials? (These two events are independent)

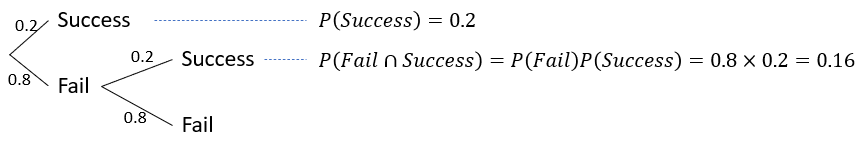
Now, what if you want to calculate the probability of winning at 100 trials?

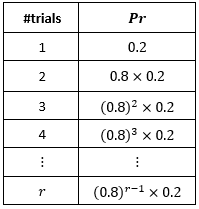
$P(X=r) = P(Fail)^{r-1} P(Success)$ where $P(Fail) = 1 - P(Success)$, termed the geometric distribution.

The geometric distribution covers situations where

1. You run a series of independent trials.
2. There can be either a success or failure for each trial, and the probability of success is the same for each trial.
3. The main thing you are interested in is how many trials are needed in order to get the first successful outcome.

Geometric distribution has the following shape:

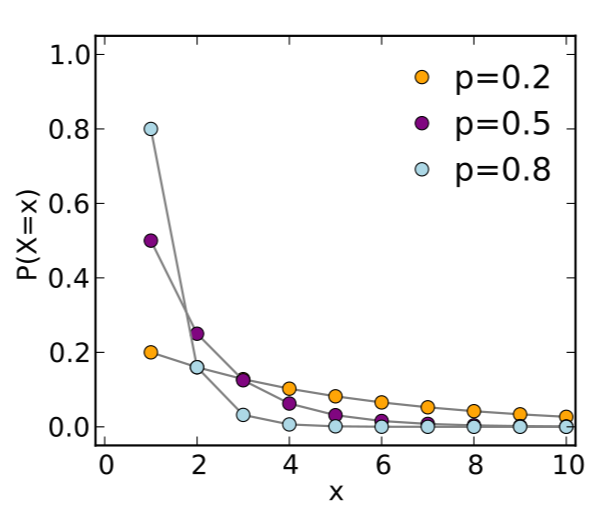
A way to calculate the probability of the geometric distribution for $P(X \le r)$

$P(X > r)$ is the probability that more than $r$ trials will be needed in order to get the first successful outcome.

$$ P(X > r) = P(Fail)^r = q^r $$

where $q$ is $P(Fail)$. Then,

$$P(X \le r) + P(X > r) = 1$$

$$ P(X \le r) = 1 - P(X > r) = 1 - P(Fail)^r = 1-q^r $$

where $P(X \le r)$ denotes the probability that the winning would happen within $r$ times.

Pattern of Expectation for the Geometric Distribution

Expectation is calculated as $\sum_i^n x_i P(x_i)$. Then the probability distribution is:

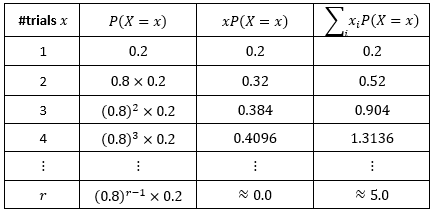
$E(X) = 5.0$. Intuitively, it makes sense since $P(Success)$ is 0.2, meaning 1 out of 5 times would be successful.

We can generalize this. If $X \sim Geo(p)$, where $p$ is $P(success)$, then,

$$ E(X) = \frac{1}{p} $$

Pattern of Variance for the Geometric Distribution

Given a quick way to calculate variance: $\frac{\sum_i^n x_i^2}{n} - \mu^2$, we can find the variance of the probability distribution by calculating 

$$ Var(X) = E(X^2) - E^2(X) $$

$$ = \sum x^2 P(X = x) - [ \sum x P(X = x) ]^2 $$

In general, if $X \sim Geo(p)$, then

$$ Var(X) = \frac{q}{p^2} $$ where $q = 1-p$

A Quick Guide to Geometric Distribution

• Probability of the first success being in the $r$-th trial: $P(X=r) = p q^{r-1}$
• Probability that you will need more than $r$ trials to get your first success: $P(X > r) = q^r$
• Probability that you will need $r$ trials or less to get your first success: $P(X \le r) = 1 - q^r$
• Expectation: $\frac{1}{p}$
• Variance: $\frac{q}{p^2}$

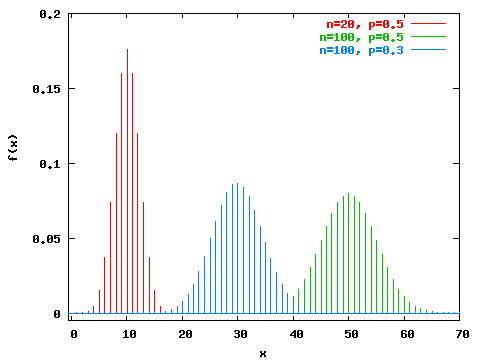
Binomial Distirbution

Example

There are 3 questions and you are going to answer randomly. What is the probability that you get $r$ questions right? (There are 4 options for each question.)

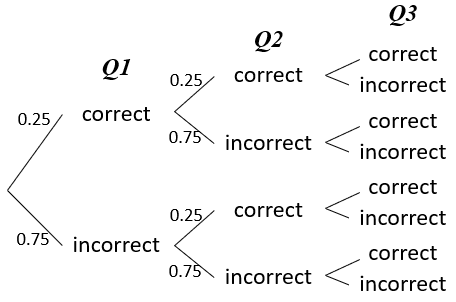
Let $X$ be a number of questions you get right:

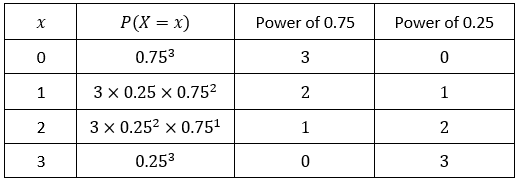
$$ P(X=r) = ^{n}C_{r} P(correct)^r P(incorrect)^{n-r} = ^{n}C_{r} p^r q^{n-r} \tag{7}$$

As for $^{n}C_{r}$, since we only care about how many questions you get right, the order does not matter, therefore, the combination is used. $Eq.(7)$ forms a binomial distribution:

Expectation and Variance of Binomial Distribution

Let's looked at one trial: 

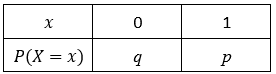
Then, 

$$ E(X) = 0q + 1p = p $$

$$ Var(X) = E(X^2) - E(X)^2 = (0q + 1p) - p^2 = p - p^2 = p(1-p) = pq $$

If we consider $n$ independent observations:

$$E(X) = np$$

$$ Var(X) = npq $$

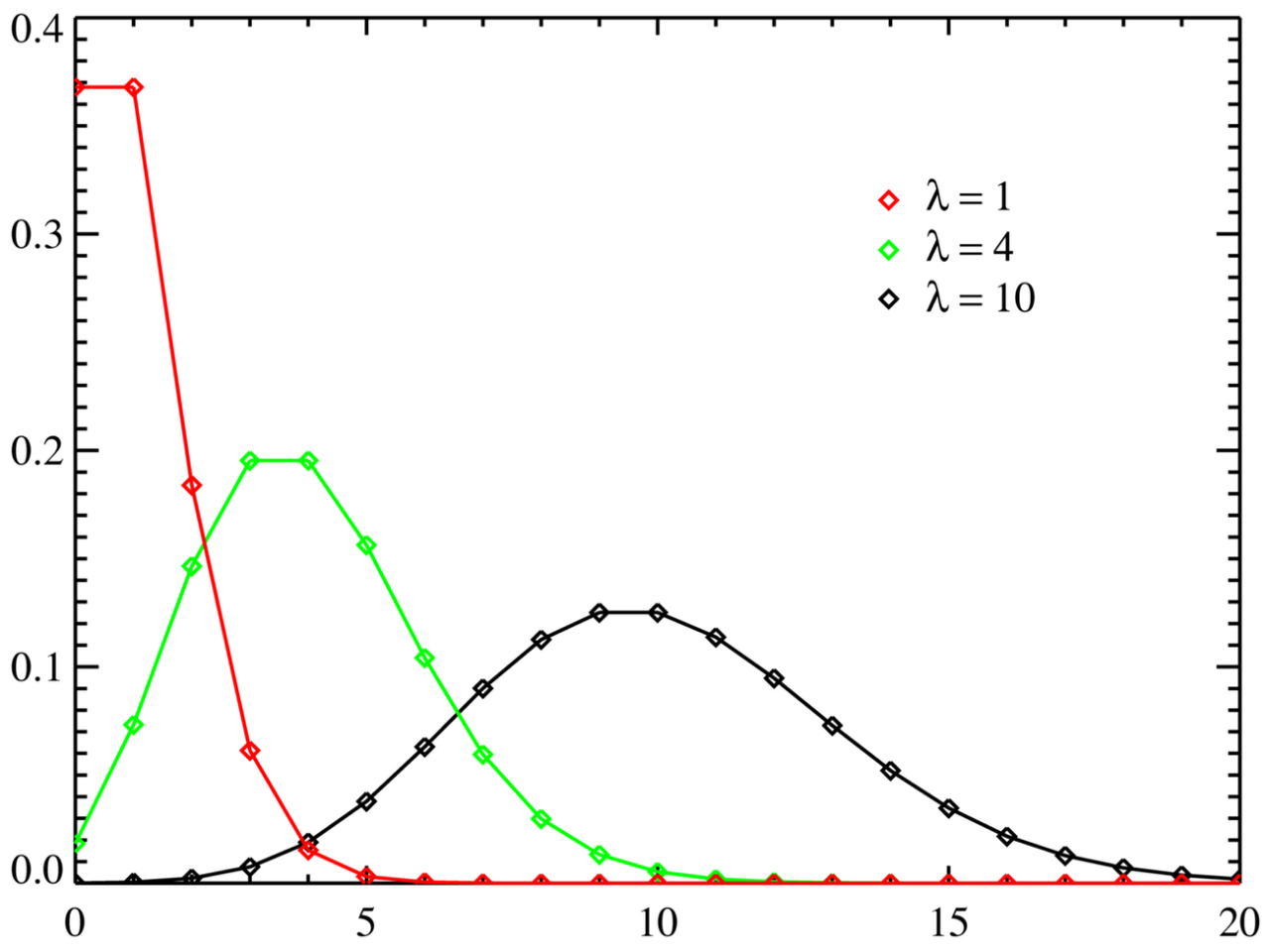
Poisson Distribution

It is used when we want to calculate the probability that there are $r$ occurrences in a specific interval (period). 

To establish the Poisson distribution, we must know the mean number of occurrences in the specific interval (period) $\lambda$. 

The Poisson distribution is represented by:

$$ P(X=r) = \frac{e^{-\lambda} \lambda^r }{ r! } $$

Example

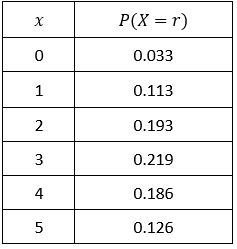
There is a popcorn machine. Its mean malfunctioning occurrences per week is 3.4. What is the probability that the popcorn machine will not malfunction next week?

$$ P(X=0) = \frac{ e^{-3.4} 3.4^0 }{ 0! } = \frac{e^{-3.4}}{1} = 0.033 $$

What about $P(X=r)$?

Expectation and Variance of the Poisson Distribution

Since $\lambda$ already represents the mean occurrences, $E(X)$ is equivalent to $\lambda$.

To make things simpler, the variance of the Poisson distribution is also the same as $\lambda$.

Estimation of the Binomial Distribution with the Poisson Distribution

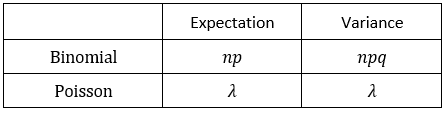
It means that the Binomial and Poisson are similar when $np = npq$, meaning if $n$ is large and $q$ is close to 1 (= $p$ is small), the two distributions are very close.

Example

A student is guessing 50 questions in an exam. The probability of getting a question right is 0.05. What is the probability that the student will get 5 questions right?

Solution: Since $n$ is large enough and $p$ is small enough, we can use the Poisson distribution to approximate the Binomial distribution.

$$ P(X=5) = \frac{e^{-\lambda} \lambda^5}{ 5! } $$

where $\lambda = 0.05 \times 50questions = 2.5$, Then,

$$ = \frac{e^{-2.5} 2.5^5 }{ 5! } = 0.668 $$ 

If we comute $P(X=5)$ by the Binomial distribution, $ ^{n}C_r p^r q^{(n-r)}$, it results in 0.0658, which is very close to the result by the Poisson distribution.

Normal Distribution

Example

The following normal distribution represents men's height. What is the probability that a man is taller than 160cm and shorter than 180cm?

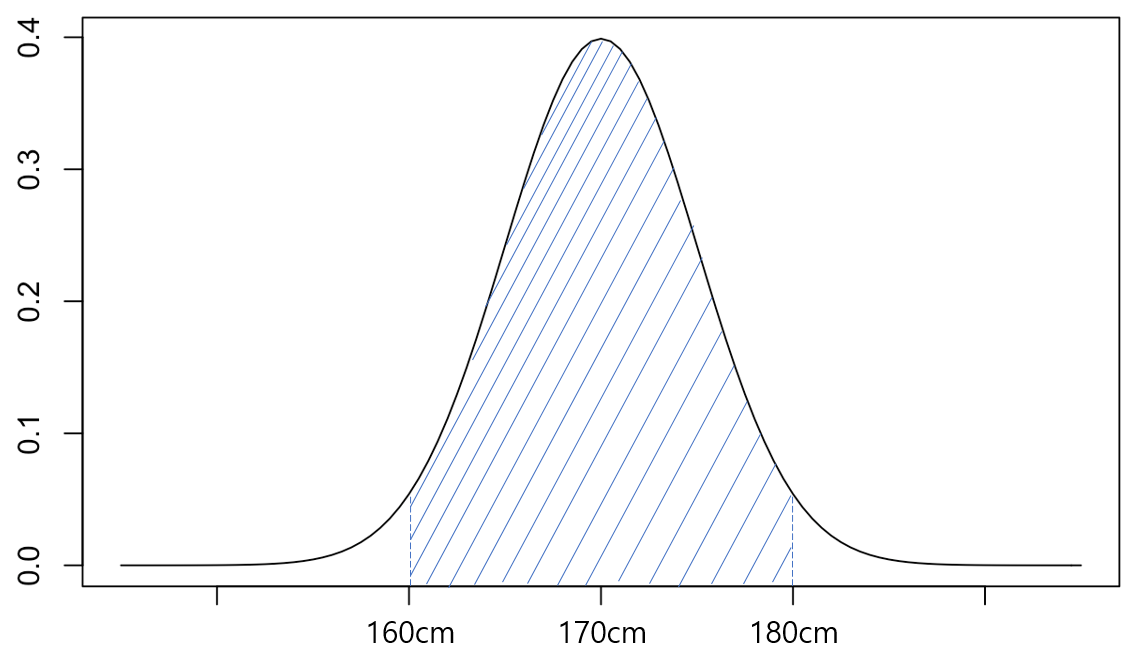
The hatched area is the probability $P(160cm \le X \le 180cm)$.

When we were working with discrete probability distributions, we saw that as long as $X$ and $Y$ are independent we could work out $E(X + Y)$ and $Var(X + Y)$ by using,

$$ E(X+Y) = E(X) + E(Y) $$

$$ Var(X+Y) = Var(X) + Var(Y) $$

Also,

$$ E(X-Y) = E(X) - E(Y) $$

$$ Var(X-Y) = Var(X) + Var(Y) $$

This can apply to the normal distribution in the same way:

$$ X \sim N(\mu_X, \sigma^2_X) + N(\mu_Y, \sigma^2_Y) = X+Y \sim N(\mu_X + \mu_Y, \sigma^2_X + \sigma^2_Y) $$

$$ X \sim N(\mu_X, \sigma^2_X) - N(\mu_Y, \sigma^2_Y) = X-Y \sim N(\mu_X - \mu_Y, \sigma^2_X + \sigma^2_Y) $$

Independent Observations of Normal Distributions

Example

A car will hold a total weight of 800 pounds. We assume the weight of an adult in pounds is distributed as:

$$ X \sim N(180, 625) $$

What is the probability that the combined weight of four adults will be less than 800 pounds?

Solution: We need to work on the probability distribution of four independent observations of $X$:

$$ X_1 + X_2 + X_3 + X_4 $$

Since the expectation and variance of independent obsrevations of discrete random variables, we found that

$$E(X_1 + X_2 + \cdots + X_n) = n E(X)$$

$$Var(X_1 + X_2 + \cdots + X_n) = n Var(X)$$

These work for continuous random variables too. That means:

$$ X_1 + X_2 + \cdots + X_n \sim N(n \mu, n \sigma^2) $$

$$ \therefore \: X_1 + X_2 + X_3 + X_4 \sim N(4 \times 180, 4 \times 625) = N(720, 2500) $$

Approximation of Binomial Distribution with Normal Distribution

Example

There are 40 multiple-choice questions (4 choices each). What is the probability of getting over 30 questions right?

• Using the Binomial distirubiton:

$$ P(30 \le X \le 40) = P(X=30) + P(X=31) + \cdots + P(X=40) $$

$$ = ^{40}C_{30} p^{30} q^{40-30} + ^{40}C_{31} p^{31} q^{40-31} + \ cdots + ^{40}C_{40} p^{40} q^{40-40} $$

However, it takes a lot of time to calculate due to the factorials.

• Using the normal distribution approaximating the Binomial distribution:

The Binomial distribution gets to have a similar distribution to the normal distribution when $p$ is close to 0.5 and $n$ is large enough. As a general rule, you can use the normal distribution to approximate the binomial distribution if

$$ np>5 \:\: and \:\: nq>5 $$

In this example, $np=10$ and $nq=30$. Since $E(X) = np$ and $Var(X) = npq$ of the binomial distribution are 10 and 7.5, respectively, the normal distribution $N(10, 7.5)$ can approximate the binomial distribution $B(10, 7.5)$.

• Continuity correction:

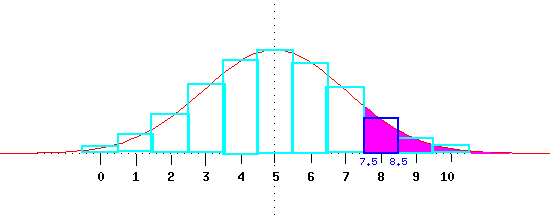
From discrete to continuous

Continuity correction table

Given the continuity correction, the answer to the question is:

$$ \therefore Area \:\: of \:\: N(29.5 \le X \le 40.5) $$

Approximation of Poisson Distribution with Normal Distribution

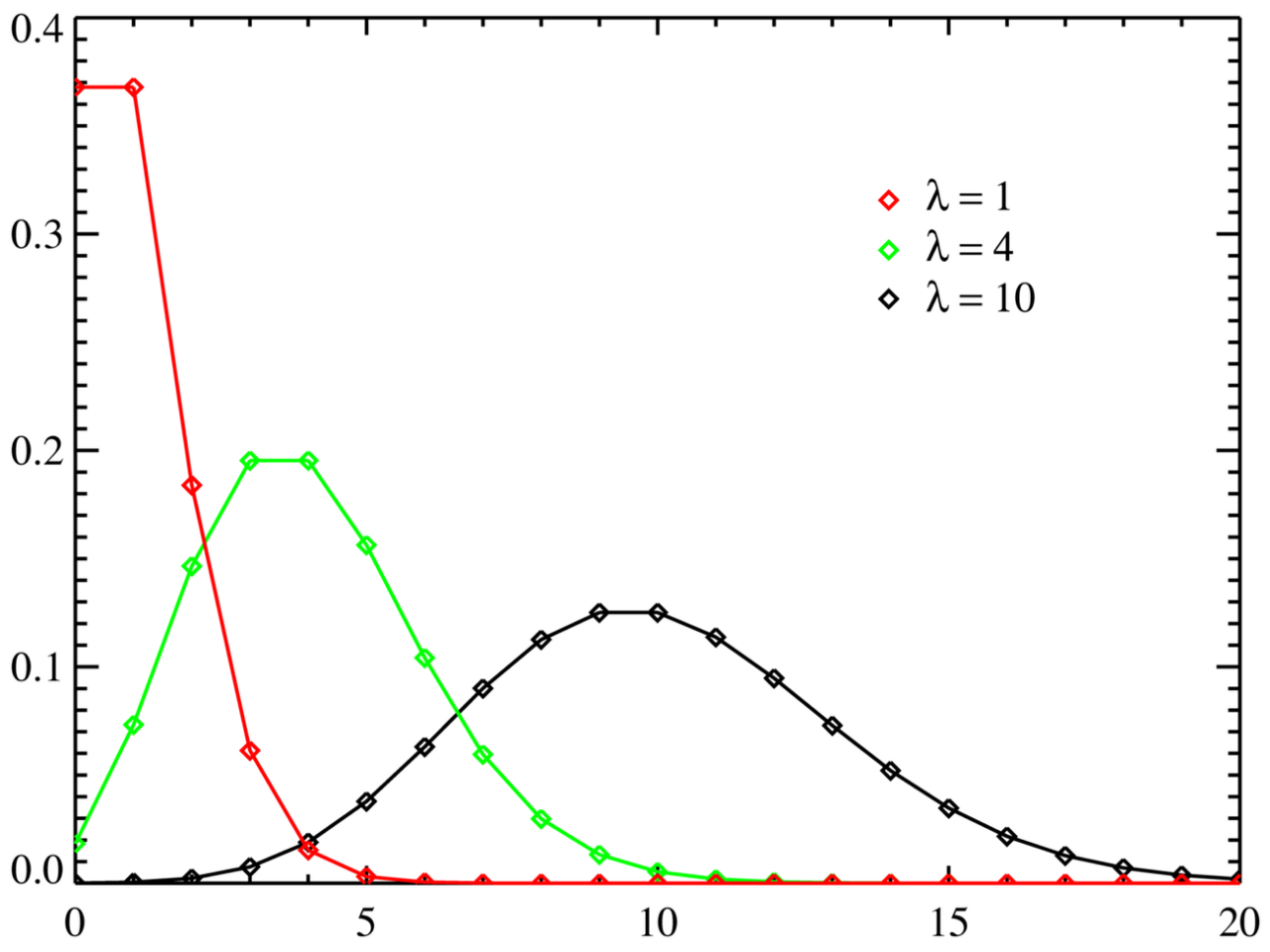
When $\lambda$ is large, the Poisson distribution looks similar to the normal distribution. In general, when $\lambda > 15$,

$Po(\lambda) \approx N(\lambda, \lambda)$

Note that $E(X)$ and $Var(X)$ of $Po(\lambda)$ is $\lambda$ and $\lambda$, respectively.

Example

A train is expected to break down 40 times a year. What is the probability that the train will break down less than 50 times a year? (= $P(X < 50)$)

Solution: $\lambda = 40$ [year] and it follows the Poisson distribution. But since $\lambda > 15$, we can use a normal distribution to approximate it:

$$ P(40) \approx N(40, 40) $$

Since we approximate a discrete probability distribution with a continuity one, we have to apply a continuity correction. Then, we have to compute: $ P(X \le 49.5) $ instead of $P(X < 50)$ for the normal distribution. 

How to Design a Sample

1. Define your target population.
2. Define your sampling units.
3. Define your sampling frame.

Sampling Methods

1. Simple Random Sampling: a) sampling with replacement, b) sampling without replacement.
2. Stratified Sampling
3. Cluster Sampling: e.g. 한봉지안에 여러가지맛이 섞여있다면, $n$ 봉지를 무작위 추출해 샘플링 수행. 이때, 봉지끼리의 여러가지 맛의 분포가 비슷해야함.
4. Systematic Sampling:  you list the population in the same sort of order, and then survey every $k$-th item.

Point Estimator

The point estimator of a population parameter is some function of calculation that can be used to estimate the value of the population. We use the hat symbol for the pint estimators. For example,

$\mu$: Population mean

$\hat{\mu}$: Point estimator of the population mean

$\hat{\mu}$: $\frac{\sum_i^n x_i}{n} = \bar{x}$: Sample mean

Then, what is the point estimator of the population variance (= sample variance)?

$$ \hat{\sigma}^2 = \frac{ \sum_i^n (x_i - \bar{x})^2 }{ n-1 } $$

Originally, the denominator is $n$. But $n-1$ is used for the sample variance since there is a high chance that $\hat{\sigma}^2 < \sigma^2$ when $n$ is small. By using $n-1$, we get a slightly greater variance ,which is likely to be closer to the population variane.

Population proportion is denoted as $P = \frac{\# successes}{ \# population }$. Then, its point estimator is $\hat{P} = P_s =\frac{ successes \: in \: the \: sample }{ number \: of \: the \: sample }$.

Sample Proportion

Let $X$ be a number of red gumballs in a sample, and there are 100 gumballs in a sample (= a box). 25% of the entire gumballs (= entire population) are red. Then,

$$ X \sim B(n, p) $$

Then, the proportion of $X$ in a sample is $X/n$, then we can define:

$$ P_s = \frac{X}{n} $$

Then, we can calculate its expectation and variance:

$$ E(P_s) = E(\frac{X}{n}) = \frac{E(X)}{n} = \frac{np}{n} = p $$

$$ Var(P_s) = Var(\frac{X}{n}) = \frac{1}{n^2} Var(X) = \frac{npq}{n^2} = \frac{pq}{n} $$

Now, we can establish the distribution. Since $(np>5, nq>5)$, we can approximate the binomial distribution with the normal distribution, $B(n,p) \approx N(np, npq)$. Then, the distribution of the sample proportion is represented as:

$$ P_s \sim N(p, \frac{pq}{n}) $$

Now, what is the probability that 40 and more gumballs are red in one particular sample?

$$ P(P_s > 0.4) $$

$$ = 1 - P(P_s \le 0.4) $$

$$ = 1 - 0.996 $$

$$ = 0.0004 $$

Sampling Distribution of the Mean

Sample mean $\bar{X} = \frac{X_1 + X_2 + \cdots + X_n}{n}$.

If you want to calculate probabilities for the sample mean, you need to know how the sample means are distributed.

Expectation of the sample mean $\bar{X}$:

$$ E(\bar{X}) = E(\frac{X_1 + \cdots + X_n}{n}) = \frac{1}{n} \{ E(X_1) + \cdots + E(X_n) \} = \frac{1}{n} n \mu = \mu $$

$$ Var(\bar{X}) = Var(\frac{X_1 + \cdots + X_n}{n}) = \frac{1}{n^2} \{ Var(X_1) + \cdots + Var(X_n) \} = \frac{n \sigma^2}{n^2} = \frac{\sigma^2}{n} $$

Central Limit Theorem

\bar{X} \sim N(\mu, \frac{\sigma^2}{n})

If you obtain a sampling distribution, it will follow the normal distribution if $n>30$.

• If $X \sim N(\mu, \sigma^2)$; $\bar{X} \sin N(\mu, \frac{\sigma^2}{n})$
• If $X \sin B(n, p); \bar{X} \sim N(\mu, \frac{\sigma^2}{n}) = N(np, \frac{npq}{n}) = N(np, pq) $
• If $X \sin Po(\lambda); \bar{X} \sim N(\mu, \frac{\sigma^2}{n}) = N (\lambda, \frac{\labmda}{n}) $

Example

The mean number of gumballs per package is 10, and its variance is 1. If you take a sample of 30 packets, what is the probabiity that the sample mean is 8.5 gumballs per packet or fewer?

Solution: We know that $\mu = 1, \sigma^2=1, n=30$. Then,

$$ \bar{X} \sim N(\mu, \frac{\sigma^2}{n}) = N(10, \frac{1}{30}) $$

Now, you compute $P(X < 8.5)$ which results in almost zero.

Confidence Interval

The company used a sample of 100 gumballs to come up with a point estimator of 62.7 minutes for the mean flavor duration, and 25 minutes for the population variance.

Instead of specifying the average flavor lasting time as 62.7 minutes, the company wants to specify an interval where the average time is likely to lie in. How can they do it?

Solution: they can use a confidence interval. People often use the 95% confidence level $\rightarrow$ $P(a \le \hat{\mu} \le b) = 0.95$. Here, $(a, b)$ is called the confidence interval.

Since we do not know the population mean $\mu$ and population variance $\sigma^2$, we esimate them with the point estimators, $\hat{\mu}, \hat{\sigma^2}$. Then,

$$ \bar{X} \sim N(\hat{\mu}, \hat{\sigma^2}) = N(62.7, \frac{25}{100}) = N(62.7, 0.25) $$

where the standard error ($SE$) is 0.5. Then, the 95% confidence interval is:

$$ (\hat{\mu} - 1.96 SE, \: \hat{\mu} + 1.96 SE) $$

$$ = (62.7 - 1.96 \ times 0.25, \: 62.7 + 1.96 \times 0.25) $$

t-Distribution

usually, the normal distribution is used for the central limit theorem. But if $n$ (a number in a sample) is small (i.e. $n<30$), we bettr use the t-distribution as it allows more uncertainty. The t-distribution takes one parameter $\nu$ (= number of degres of freedom). It is calculated as $(n-1)$ for the t-distribution:

$$ \nu = n - 1 $$

The shape of the t-distribution is as follows:

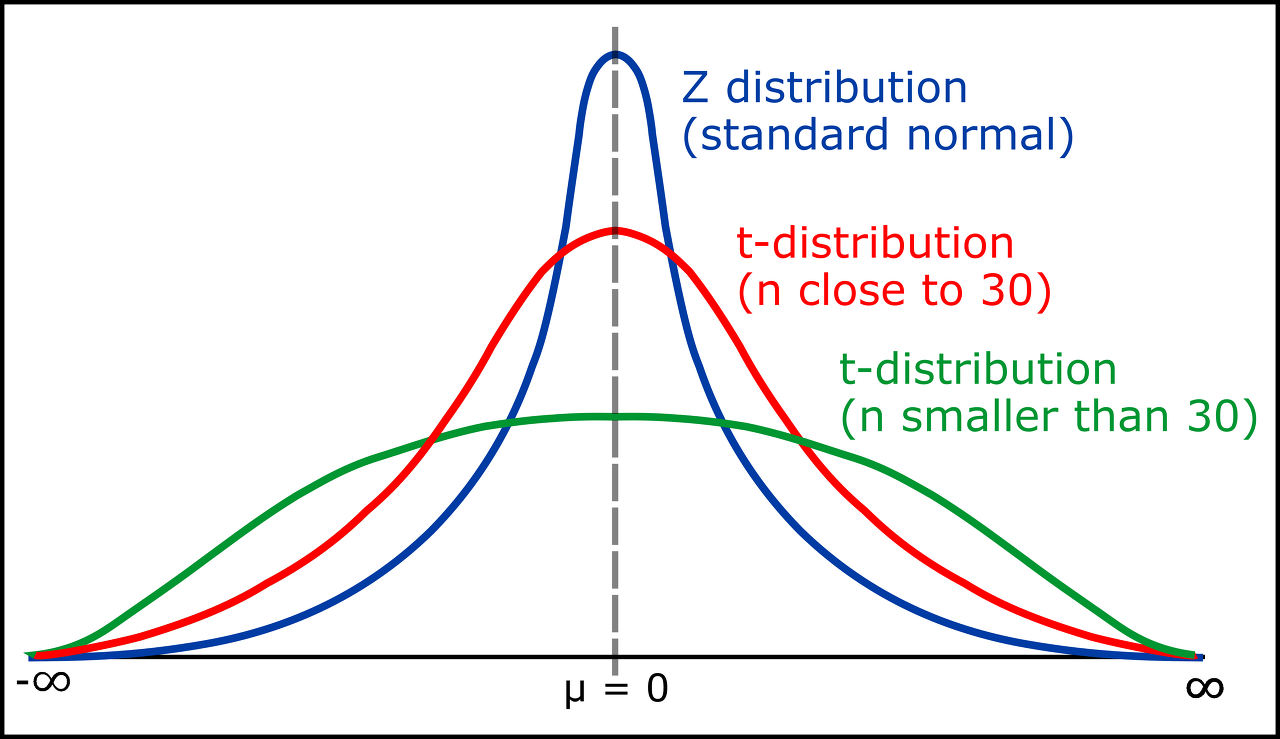
t-distribution

Hypothesis Test

It is a test to see if a claim is statistically correct or not. Here are the steps for the hypothesis test:

1. Decide on the hypothesis you are going to test.
2. Choose your test statistic.
3. Determine the critical region.
4. Find the $p$-value.
5. See whether the sample is within the critical region.
6. Make your decision.

Example

A drug company claims that its new drug has a success rate of 90%. But some doctor conducted a test with 15 patients and got the following result:

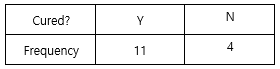
Run the hypothesis test:

1. Decide on the hypothesis.

    null hypothesis $H_0$; $p=0.9$

    alternative hypothesis $H_1$; $p<0.9$

2. Choose your test statistic.

    $X \sim B(n, p)$ where $X$ denotes #cured, $n$ is 15, and $p$ is 0.9. Note that since $nq<5$, we cannot use the normal distribution to approximate it. So, according to the drug company, $X$ should follow $X \sim B(15, 0.9)$.

3. Determine the critical region.

    Let the significance level $\alpha$ be 5%. Then,

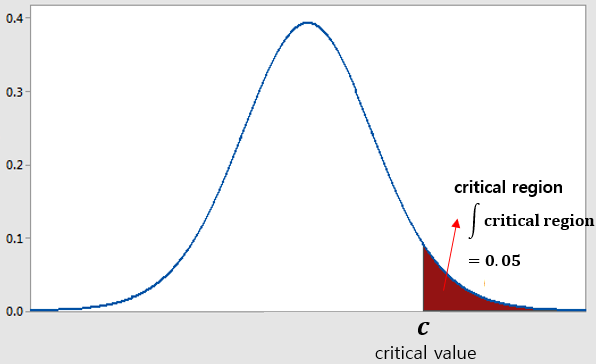
    If the sample lies within the critical region, we can reject $H_0$.

4. Find the $p$-value.

    According to the doctor's test, $X=1$. Then, the $p$-value is $P(X \le 11)$.

5. See whether the sample is within the critical region.

$$ P(X \le 11) = 1 - P(X \ge 12) = 1 - \left[ P(X=12) + \cdots + P(X=15) \right] = 0.0555 $$

6. Make a decision.

    Since the $p$-value is outside of the critical region, we cannot reject $H_0$, meaning the drug company's claim still stands.

Example

The doctor conducted an additional test and got the following result:

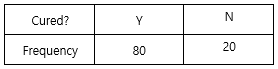
Now, $n$ is 100, the test statistic is 

$$ X \sim B(100, 0.9) \approx N(np, npq) $$

where the binomial distribution could be approximated by the normal distribution since $np>5$ and $nq>5$.

The $p$-value of the new sample is $P(X \le 80) = 0.0004$. Since the $p$-value is within the critical region, we can reject $H_0$.

Errors in the Hypothesis Test

Type 1 error: $P(Type \: 1 \: error) = \alpha$

Type 2 error: We can find $P(Type \: 2 \: error)$ using the test statistic described by $H_1$ instead of $H_0$.

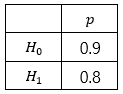
Therefore, we can build the test statistic as

$$ X \sim N(\mu, \sigma^2) = N(np, npq) = N(100 \times 0.8, \: 100 \times 0.8 \times 0.2) = N(80, 16) $$

Since the critical value was 85.08, $P(Type \: 2 \: error)$ can be calculated as follows:

Finally, $P(Type \: 2 \: error) = \beta = P(X \ge 85.08) = 0.102$ where $X \sim N(80, 16)$.

Power of a Hypothesis Test

It is the probability that you would correctly reject $H_0$:

\Power = 1 - \beta = 0.898\

$\chi^2$ distribution

Let's say there is a slot machine with the following expected probability distribution:

Expected probability distribution

Observed frequency

Then, we can make the following table:

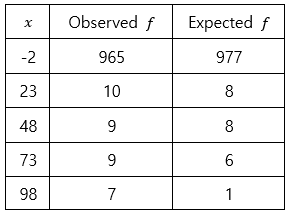
Now, we can calculate $X^2$:

$$ X^2 = \sum \frac{(O - E)^2}{E} = 38.272 $$

where $O$ and $E$ denote observed and expected, respectively. This $X^2$ gives a way of measuring the difference between the frequencies we observe and expect.

So, at what point does $X^2$ become so large that it is statistically significant? To find that out, we use the $\chi^2$ distribution. 

$$ X^2 \sim \chi^2(\nu) $$

$\chi^2$ distribution mainly has two purposes: 1) To test goodness of fit, 2) To test the independence of two variables. Here, we utilize it for the first purpose. $\chi^2$ distribution has one parameter $\nu$ called a number of degrees of freedom (= number of classes - number of restrictions).

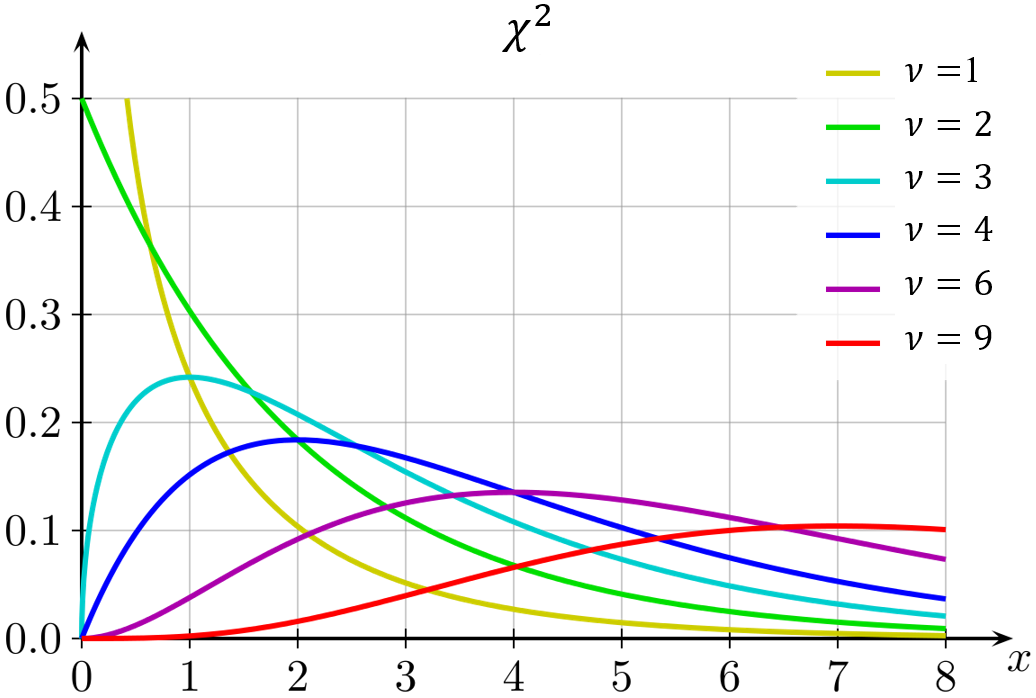
$\chi^2$ distribution with different $\nu$

We set a significance level $\alpha$ (e.g. 5%), then,

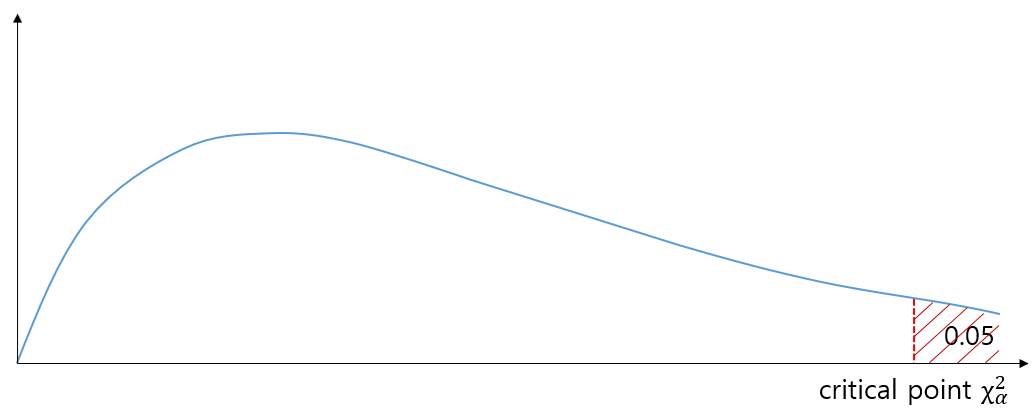
$\therefore$ If $X^2$ from the sample is within the critical region, we can reject $H_0$ that the observation follows the expected probability distribution.

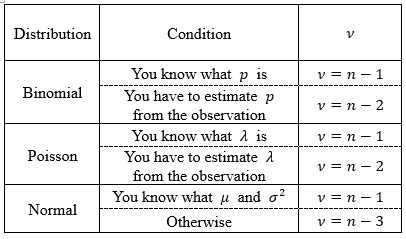
The hardest thing is using the $\chi^2$ distribution is working out what $\nu$ (= #degrees of freedom) should be. ere are $\nu$ for some of the most common distributions:

$\chi^2$ Distribution to Test Independence

A guy has been gambling with 3 croupiers, and he has a suspicion that one of the croupiers has been cheating. How do we know?

Solution: We can figure it out by testing whether the outcome of the game is dependent on which croupier is leading the game.

The observation is as follows:

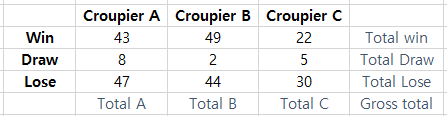
Then, the expected probabilities are:

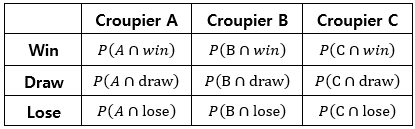
Assuming that the outcomes and the croupiers are independent, $P(A \cap win) = P(A)P(win)$, $P(B \cap win) = P(B) P(win)$, and so on, in which $P(A) = \frac{Total \; A}{Gross \; total}$, $P(win) = \frac{Total \; win}{Gross \; total}$, and so on.

Once we calculate all the expected frequencies, we can compute $X^2$,

$$ X^2 = \sum \frac{(O - E)^2}{E} $$

Before we calculate $\chi_{\alpha}^2 (\nu)$, we have to know $\nu$. There are 4 pieces of independent information we have to calculate, the other 6 are automatically known. Refer to the following figure:

Therefore, for this example, $\nu = 4$.

If we set the significance level to 1%, then

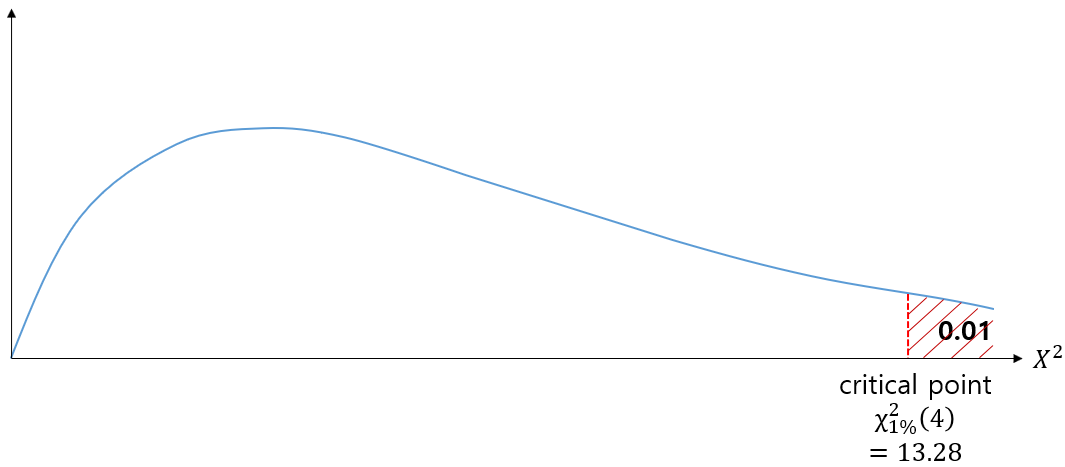
$\therefore$ since $X^2 = 5.004$, it is outside of the critical region, meaning that we cannot reject $H_0$.