Odds Ratios and Log(Odds Ratios)

Odds

The chance of my team winning is 0.33, then the chance of my team losing is 0.67. Its odds are computed as

$$odds = \frac{0.33}{0.67} = 0.493$$

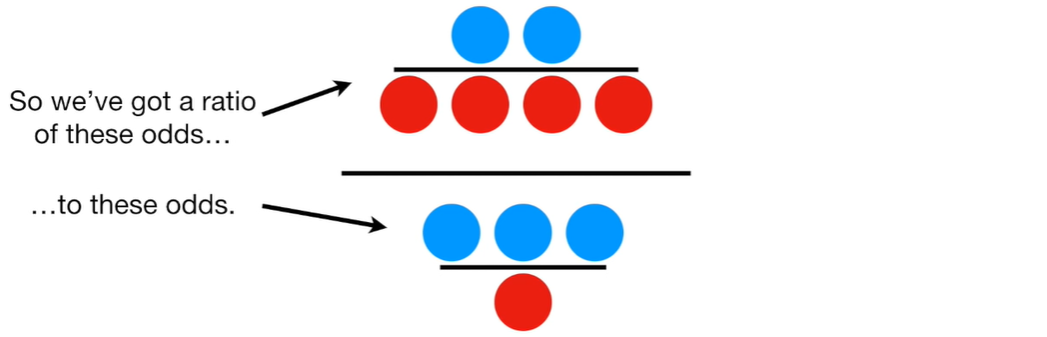
Odds Ratio

"Odds ratio" is different from the odds. It is a ratio of odds.

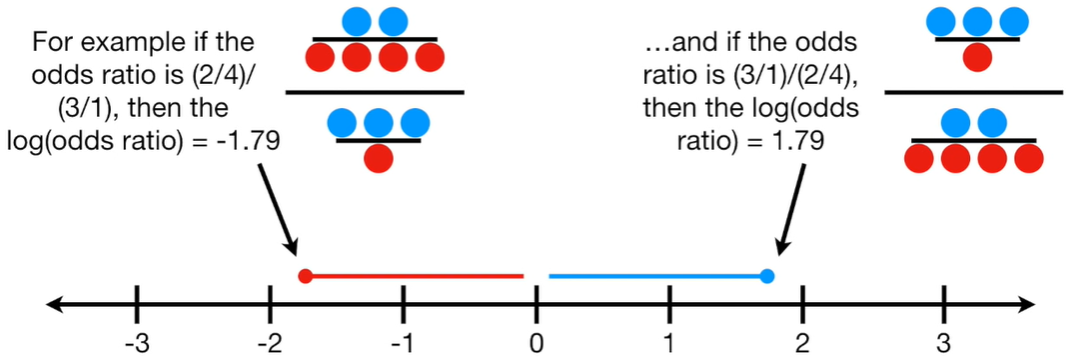
Log(Odds Ratio)

If the denominator is larger than the numerator the odds ratio will go from 0 to 1. If the numerator is larger than the denominator, then the odds ratio will go from 1 to infinity. The log of the odds ratio makes things nice and symmetrical:

Example of the Odds Ratio

We can use the odds ratio to determine if there is a relationship between the mutated gene and cancer. Given a person has the mutated gene, the odds that the person has cancer are $23/117$. Given that a person does not have the mutated gene, the odds that the person has cancer are $6/210$. Then, our odds ratio is:

$$\frac{ \frac{23}{117} }{ \frac{6}{210} } = \frac{0.2}{0.03} = 6.88$$

$$\log(6.88) = 1.93$$

The odds ratio and the log(odd ratio) are like the r-squared score. They indicate a relationship between two things (in this case, a relationship between the mutated gene and cancer). The larger values mean that the mutated gene is a good predictor of cancer, Smaller values mean that the mutated gene is not a good predictor of cancer.

 

Reference: Youtube video, "StatQuest: Odds Ratios and Log(Odds Ratios), Clearly Explained!!!"