F-ratio (F-statistic), F-distribution, and F-test

We need the $F$-ratio ($F$-statistic) and $F$ distribution to compare two random variable's variability. Thus, the question we're trying to answer using these is "Are two variances $\sigma_x$ and $\sigma_y$ from the same population?".

The $F$-ratio measures the variability:

$$F=\frac{s_x^2}{s_y^2}$$

where $s_x^2$ and $s_y^2$ denote larger sample variance and smaller sample variance, respectively. Intuitively speaking, if the two variables are from the same population, $F$-ratio should be close to 1. 

The $F$-distribution is a distribution of the $F$-ratios. The distribution has two parameters: 1) degrees of freedom for $s_x^2$, 2) degrees of freedom for $s_y^2$, where the degrees of freedom is calculated as (a number of a sample - 1).

Once you know the two degrees of freedom, you can establish the $F$-distribution, and calculate a critical value according to the significance level $\alpha$ (e.g. 5%).

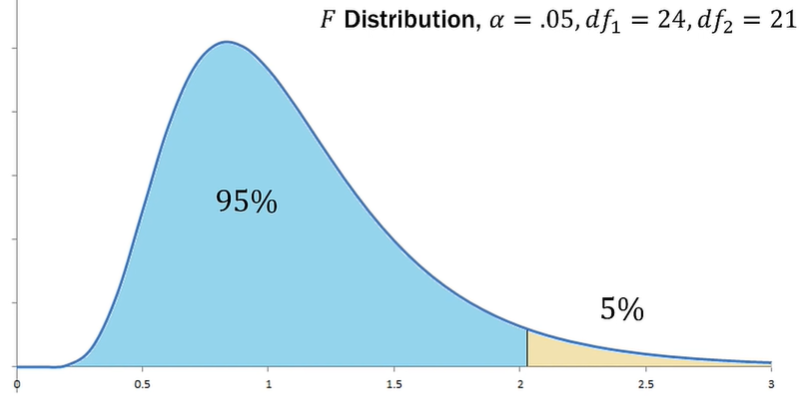
If the $F$-ratio lies within the critical region, you can reject the null hypothesis ($\rightarrow$ this process is called $F$-test). 

 

source: this tutorial video