[PyTorch] .detach() in Loss Function
What happens if you put .detach() in a loss function? Like in the SimSiam algorithm:

Example 1
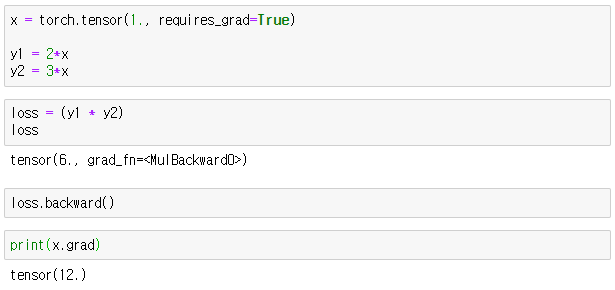
Let's say, we have the following equations:
$$ J = y_1 y_2 $$
$$ y_1 = 2 x $$
$$ y_2 = 3 x $$
Then, naturally, the derivatives of $J$ w.r.t the $x$ are:
$$ J = (2x) (3x) = 6x^2 = 12x $$
However, if .detach() is applied to $y_1$, we treat $y_1$ as a constant when computing derivatives:
$$ \frac{\partial J}{\partial x} = (y_1) (y_2)^{\prime} = (2x) (3) $$
PyTorch Implementation

Example 2
Let's say, we have the following equations:
$$ J = y_1 y_2 $$
$$ y_1 = x_1 + x_2 $$
$$ y_2 = 2 x_1 + 3 x_2 $$
Then, naturally, the derivatives of $J$ w.r.t the $x$ are:
$$ J = (x_1 + x_2) (3 x_1 + 3 x_2) $$
$$ = 2 x_1^2 + 5 x_1 x_2 + 3 x_2^2 $$
$$ \frac{\partial J}{\partial x_1} = 4 x_1 + 5 x_2 $$
$$ \frac{\partial J}{\partial x_2} = 5 x_1 + 6x_2 $$
However, if .detach() is applied to $y_1$, we treat $y_1$ as a constant when computing derivatives:
$$ \frac{\partial J}{\partial x_1} = (y_1) (y_2)^{\prime} = (x_1 + x_2) (2) $$
$$ \frac{\partial J}{\partial x_2} = (y_1) (y_2)^{\prime} = (x_1 + x_2) (3) $$
PyTorch Implementation

